Annex A - Cinematic Analysis
This annex is intended to study the kinematic motion of the four-bar linkage. The final objective of this
section is to find two direct relations to calculate γ and δ depending on θ with a fixed linkage geometry.
Some fundamental variables are defined as follows:
\[\begin{split}\begin{array}{ll}
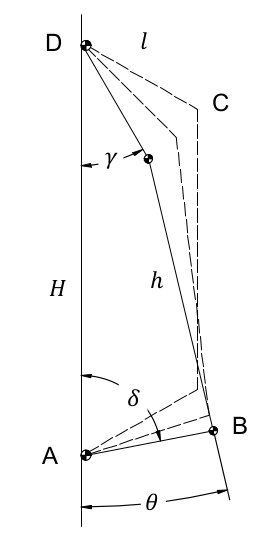
H & \mbox{the frame AD;} \\
l & \mbox{the two rockers AB e CD;} \\
h & \mbox{the coupler BC;} \\
\gamma, \delta & \mbox{the actual angles between the frame and the rockers;} \\
\theta & \mbox{the angle formed by the coupler and the frame, with a positive} \\
& \mbox{sign when the antenna points downwards.}
\end{array}\end{split}\]
The following equations come from simple geometric considerations:
\[\begin{split}\begin{array}{lr}
\begin{cases}
H = l \cdot \cos\gamma + h \cdot \cos\theta + l \cdot \cos\delta \\
l \cdot \sin\delta = l \cdot \sin\gamma + h \cdot \sin\theta
\end{cases} &
(A.1)
\end{array}\end{split}\]
rearranging the equations, the following can be obtained:
\[\begin{split}\begin{array}{lr}
\begin{cases}
l \cdot (\cos\gamma + \cos\delta) = H - h \cdot \cos\theta \\
l \cdot (\sin\gamma - \sin\delta) = h \cdot \sin\theta
\end{cases} &
(A.2)
\end{array}\end{split}\]
extracting l and replacing it in the first equation, it results as:
\[\begin{array}{lr}
h \cdot \sin\theta \frac {(\cos\gamma + \cos\delta)} {(\sin\gamma - \sin\delta)} = H - h \cdot \cos\theta &
(A.3)
\end{array}\]
using sum to product identities:
\[ \begin{align}\begin{aligned}\begin{array}{lr}
\cos\alpha + \cos\beta = 2 \cos(\frac {\alpha + \beta} 2) \cdot \cos(\frac {\alpha - \beta} 2) &
(A.4)
\end{array}\\\begin{array}{lr}
\sin\alpha - \sin\beta = 2 \sin(\frac {\alpha - \beta} 2) \cdot \cos(\frac {\alpha + \beta} 2) &
(A.5)
\end{array}\end{aligned}\end{align} \]
it is possible to write the following:
\[\begin{array}{lr}
\frac {\cos\gamma + \cos\delta} {\sin\gamma - \sin\delta} = \frac {2 \cos(\frac {\gamma + \delta} 2)
\cdot \cos(\frac {\gamma - \delta} 2)} {2 \sin(\frac {\gamma - \delta} 2) \cdot 2 \cos(\frac {\gamma + \delta} 2)}
= \cot (\frac {\gamma - \delta} 2) &
(A.6)
\end{array}\]
and to obtain first key equation:
\[\begin{array}{lr}
\tan (\frac {\gamma - \delta} 2) = \frac {h \cdot \sin\theta} {H - h \cdot \cos\theta } &
(A.7)
\end{array}\]
Going back to the (A.2), since both the members of the two equations are positive, squaring will not produce
a change in the result:
\[\begin{split}\begin{array}{lr}
\begin{cases}
l^2 \cdot (\cos\gamma + \cos\delta)^2 = (H - h \cdot \cos\theta)^2 \\
l^2 \cdot (\sin\gamma - \sin\delta)^2 = h^2 \cdot \sin^2 \theta
\end{cases} &
(A.8)
\end{array}\end{split}\]
expanding the squares:
\[\begin{split}\begin{array}{lr}
\begin{cases}
l^2 \cdot (\cos^2 \gamma + \cos^2 \delta + 2\cos\gamma\cdot\cos\delta) = H^2 - 2H \cdot h \cdot \cos\theta
+ h^2 \cdot \cos^2 \theta\\
l^2 \cdot (\sin^2 \gamma + \sin^2 \delta - 2\sin\gamma\cdot\sin\delta) = h^2 \cdot \sin^2 \theta
\end{cases} &
(A.9)
\end{array}\end{split}\]
and summing them together:
\[\begin{array}{lr}
l^2 \cdot (2 + 2\cos\gamma\cdot\cos\delta - 2\sin\gamma\cdot\sin\delta) = H^2 + h^2 -2H \cdot h \cdot \cos\theta &
(A.10)
\end{array}\]
using the difference identity:
\[\begin{array}{lr}
\cos(\gamma + \delta) = \cos\gamma \cdot \cos\delta - \sin\gamma \cdot \sin\delta &
(A.11)
\end{array}\]
it’s possible to obtain the second key equation:
\[\begin{array}{lr}
\cos(\gamma + \delta) = \frac {H^2 + h^2 - 2H \cdot h \cos\theta} {2 \cdot l^2} - 1 &
(A.12)
\end{array}\]
Now, combining the (A.7) with the (A.12), the following system of equations results:
\[\begin{split}\begin{array}{lr}
\begin{cases}
\tan (\frac {\gamma - \delta} 2) = \frac {h \cdot \sin\theta} {H - h \cdot \cos\theta} = P \\
\cos (\gamma + \delta) = \frac {H^2 + h^2 - 2H \cdot h \cdot \cos\theta} {2 \cdot l^2} -1 = Q
\end{cases} &
(A.13)
\end{array}\end{split}\]
that brings to the final result:
\[ \begin{align}\begin{aligned}\begin{array}{lr}
\gamma = \frac {2 \tan^{-1}P + cos^{-1}Q} 2 &
(A.14)
\end{array}\\\begin{array}{lr}
\delta = \frac {\cos^{-1}Q - 2 \tan^{-1}P} 2
(A.15)
\end{array}\end{aligned}\end{align} \]